Category Archives: Propagation

Decoding the Entire DGPS Band At Once, Part 2

Posted on by
Reply

In my earlier post, I introduced a new program that decodes the entire DGPS band at once, from SDR recording files. This allows you to record the band overnight, then process the recordings in the morning, to see what stations were received.

I’ve since re-written the app, with a few additions.

The big change is the ability to decode from regular WAVE audio files, if you do not have an SDR. The app can decode from multiple DGPS channels in the same WAVE file, as many as fit in the bandwidth. So if, for example, your radio is tuned to 300 kHz USB with a bandwidth of 6 kHz, then 301 to 305 kHz fit inside and will be decoded. You could of course tune to say 299.5 kHz and squeeze in another channel. Or make the bandwidth wider. Or both!

The graph window now shows a red graph at the top, which indicates the total number of messages per minute being decoded. It can be handy as a rough guide as to how well band conditions are.

I have also added support for a few other formats of SDR recordings, Studio1, ELAD, and Sdr-Radio, in addition to SdrDx / RF Space and Perseus formats. Note that I do not have all of these programs, so testing was done with files provided by others. I think it is all working correctly, but you never know.

The app is still Mac only, but the changes to this version (which is close to a complete re-write) move me closer to being able to release a Windows version. It can be downloaded here: http://www.blackcatsystems.com/software/dgps_decoding_software_sdr.html

DX Toolbox 4.3.0 Released

Posted on by
Reply

Version 4.3.0 of DX Toolbox, the radio propagation app for Windows and Mac OS X has been released.

This version adds the Ionosonde Plot Window. This window lets you see graphs of ionosonde data from a number of sites around the world. Select the site from the first popup menu (there are dozens of sites around the world), then select the type of graph from the second. There are three types:

foF2: This is a plot of the highest frequency that will be reflected from the F2 layer of ionosphere when transmitted straight up. As the incident angle is decreased, higher frequencies will be reflected, that is, more distant stations can be heard, or alternatively, more distant locations can receive the signal. This effect explains the “skip zone” around a transmitter site.

foEs: This is a plot of the highest frequency that will be reflected from the E layer of the ionosphere.

hmF2: This is a plot of the height of the F2 layer of the ionosphere. Along with the foF2 value, it can be used to calculate the MUF for a given path.

Here is a screenshot of what the window looks like, click on it to see it full sized:

DX Toolbox also displays a variety of other information, here is the main window of current space weather:

There is also this chart of recent solar and geomagnetic conditions:

Several propagation forecasting tools are also available. This one computes the MUF (maximum usable frequency) and LUF (lowest usable frequency) between two locations, as well as the estimated received signal levels:

You can read more about DX Toolbox here, and see more screenshots here.

Copies of DX Toolbox for both Windows and Mac OS X can be downloaded from the download page.

An version (minus a few features) is also available for the iPhone and iPad.

Homeopathic Radio Engineering

Posted on by
2

Mainstream radio engineering principles hold that the received signal strength of a transmission is proportional to the radiated power. Doubling the transmitter power produces twice the received power, quadrupling the transmitter power produces four times the received power, twice the received voltage, which is 6 dB or one S unit. This has been accepted for over a century.

However, recent experimental results, first reported on the FRN and later in The Journal of Irreproducible Results cast doubt in this basic radio engineering theory.

These results claim that as the transmitter power is reduced to very low levels, the received signal strength actually goes up, not down.

A transmitter location on the east coast of the USA was used. The tests were conducted on HF radio frequencies on and around 6925 kHz, using a state of the art solid state transmitter with a standard off the shelf MOSFET as the RF final amp:

Each monitoring post was equipped with the highest quality HF receiving gear and highly sensitive monopole receiving antennas.

During the trials, it was found that placing a non-conductive fabric, such as a sock, over the receiver produced the strongest signals. While the exact mechanism for this effect is not yet known, it is presumed to be due to the high dielectric constant of the fabric.

The results of the experiment clearly speak for themselves, as transmitter power went down, the signal strength went up:

One way to explain the results is to return to the luminiferous ether theory of radio propagation. Radio waves are propagated by vibrations in the ether. Fewer radio waves means that there is more ether per radio wave, so the vibrations are larger, producing a stronger signal at the receiving site.

There were even reports of radio propagation that cannot be explained by any known laws of physics, such as signals in the daytime traversing from Montana to New Zealand on 6955 khz with a completely sunlit path, even though D layer absorption would make this completely impossible. Yet this was reported many times by longtime radio physicist Dr. Winston: “The signals were always received with as SIO of 555. Even the audio quality was perfect, why it sounded like I was listening to it live in the studio!”.

Several times signals were actually received and logged on the FRN before the transmission began. This suggests that superluminal neutrinos may be involved.

Further research into this new phenomena is required. If homeopathic radio is ever perfected, it would allow listeners to report hearing transmissions that used little, or theoretically even no power. Indeed, reducing the output power to zero watts might produce the best results of all for this type of station.

Boom Box Radio Early Morning Propagation Analysis

Posted on by
Reply

Boom Box Radio had an early morning transmission on March 10, 2013, from 1044 until 1212 UTC. They were trying to reach a listener in Guatemala. The time of this transmission, starting just before to after sunrise, lets us examine the effects of sunrise on reception on the 43 meter band.

This first waterfall shows when Boom Box Radio signed on at 1044 UTC. You can see a very faint trace appear on the waterfall about a quarter of the way up from the bottom, at 6925 kHz. Remember that with a waterfall, time flows or falls down, like with a real waterfall, so the latest information is at the top:

This next waterfall shows what happened at 1107 UTC, when the signal went from just a faint trace of a carrier on the waterfall, and no audio, to a very good S7 to S9:

Note again that the oldest information as at the bottom of the waterfall. At that time, there is just barely a carrier. Then you start to see some modulation, and then finally, in a matter of seconds, the signal shoots up to armchair quality.

Below is a graph showing the signal strength of Boom Box Radio, in dBm, from 1044 UTC sign on, until 1212 UTC sign off. You can click on it to see a larger version:

An S9 signal corresponds to -73 dBm. Every S unit is 6 dBm, so S8 is -79 dBm, S7 is -85 dBm, etc.

I have annotated several important times: The 1044 UTC sign on, 1107 UTC when the signal went up, 1125 UTC which was local sunrise, and 1212 UTC when it went off the air.

You can see that there is a very slow increase in signal level after the sign on, but the signal remains extremely weak. Then suddenly at 1107 UTC, the signal shot up to S9. Then for the rest of the transmission it mostly stayed in a range between S7 and S9.

The sudden increase in signal was caused by the Sun increasing the ionization level of the F layer of the ionosphere. This increase needs to have occurred at the point in the ionosphere where the radio waves are being reflected, most likely roughly midway between the transmitter and receiver locations. Note that in my case, this occurred before my local sunrise. This could be due two at least two factors I can think of. First, the transmitter site could be to my east. Second, the ionosphere is several hundred miles up, so it experiences sunrise before a point directly below it (on the Earth’s surface) does.

I believe this graph shows the importance of selecting the correct time for transmissions, depending on your target area. Just before sunrise is when the ionosphere is the weakest, and is only able to reflect radio waves on 43 meters at low angles. Too early in the morning, and the band is not open for local (NVIS – Near Vertical Incidence Skywave) reception. The band is, however, open for reception to more distant locations, that is, more than many hundreds of miles away (well over 500, perhaps close to 1,000 miles). If you’re trying to get out to DX locations, this is a good time to do it. Sunrise varies throughout the year, so as we move into summer, and it occurs earlier, the band will likewise open up earlier for NVIS. Likewise in the middle of winter in December, it is somewhat later.

For reference, the operator of Boom Box Radio stated that this was a Heathkit DX-60 transmitter putting out 40 watts into a 40 meter band dipole that was about 15 feet high.

I thank Boom Box Radio for conducting this early morning test.

Update: The operator contacted me again to mention that his local sunrise was at exactly 1107 UTC.

WWV and WWVH Via Both Long and Short Path on 15 MHz and I can Hear Russia From My House

Posted on by
Reply

In Measuring The Distance To A Shortwave Radio Station we looked at how the propagation delay in a shortwave signal can be used to estimate the distance to the station.

I ran some more tests the other day:

Below is a recording of 15 MHz, taken at 2300 UTC on December 13, 2012:

The GPS 1 PPS reference is on the top trace, and the audio from the radio is on the lower trace.

You can see the one second tick pulse from WWV in the audio, as well as two pulses from WWVH, the first (weaker) one is the normal (short) path signal, and the second one is via long path. We can confirm this is the case by converting the time delays into distance. We’ll use the same formula as in the previous article, we subtract off the 286 sample delay from the radio, multiply by 22.676 to convert the delay in samples to microseconds, then multiply by 0.186282 (the speed of light in miles per millisecond) to convert the delay into miles.

For WWV, the measured delay from the 1 PPS pulse is 660 samples. (660-286) * 22.676 * 0.186282 = 1580 miles
For WWVH short path, the measured delay was 1516 samples: (1516-286) * 22.676 * 0.186282 = 5196 miles
For WWVH long path, the measured delay was 5080 samples: (5080-286) * 22.676 * 0.186282 = 20250 miles

The distance to WWV is 1480 miles, and to WWVH is 4743. The long path distance to WWVH is 20158 miles.

Remember, the calculated distances can be longer than the great circle distance, due to the signal making one or more (many more in the case of long path) hops between the Earth and the ionosphere. Plus, there is the experimental error.

And here is one more example, this time it is the Russian time station RMW, on 14996 kHz, recorded at 1157 UTC on December 10, 2012:

The delay was 1835 samples: (1835-286) * 22.676 * 0.186282 = 6543 miles.
The great circle distance is 4821 miles.

Measuring The Distance To A Shortwave Radio Station

Posted on by
3

In a previous post, I showed how it was possible to crudely measure the speed of light (or at least another type of electromagnetic radiation, radio waves, in this case) by measuring the time delay between two shortwave radio time stations, WWV and WWVH.

I’ve decided to re-do that experiment, but in a slightly different way. Rather than measure the speed of propagation, I will use that speed to determine the distance to the radio station.

Various time stations transmit precise time on several shortwave frequencies. Here in the USA, we have WWV in Ft. Collins, Colorado, which transmits on 2.5, 5, 10, 15, and 20 MHz. We also have WWVH in Kekaha, Hawaii, which transmits on 2.5, 5, 10, and 15 MHz. These stations transmit an audio “tick” at exactly each UTC second. There is also the Canadian station CHU, located near Ottawa, Ontario, which transmits on 3330, 7850, and 14670 kHz.

One way to measure the speed of radio waves (and light) would be to measure how long it takes for the tick to travel a fixed distance. Divide the distance by the time, and we have the speed of light. However, that requires knowing the exact UTC time locally. This can be done with a GPS unit that outputs a 1 PPS (pulse per second) signal.

How to feed these signals into the computer, so they can be measured? The radio audio is easy enough, feed it into the sound card. It turns out the 1 PPS signal can also be fed into the sound card, on the other channel. I used a capacitor to couple it.

The first measurement that is required is one to determine what time delay is added by the radio electronics. In my case, I was using a JRC NRD 545 receiver, which has DSP (Digital Signal Processing) to implement the audio filters. This certainly adds a time delay. I therefore needed to run some baseline measurements, to determine how long this delay was.

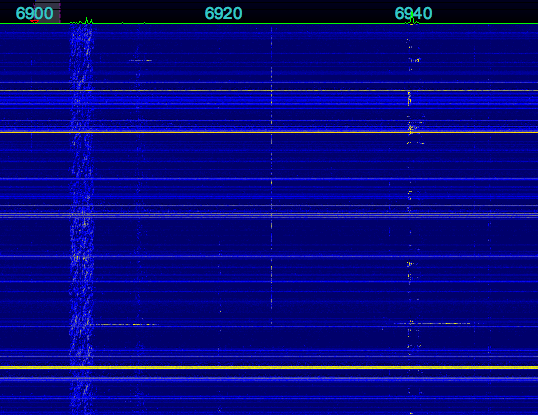
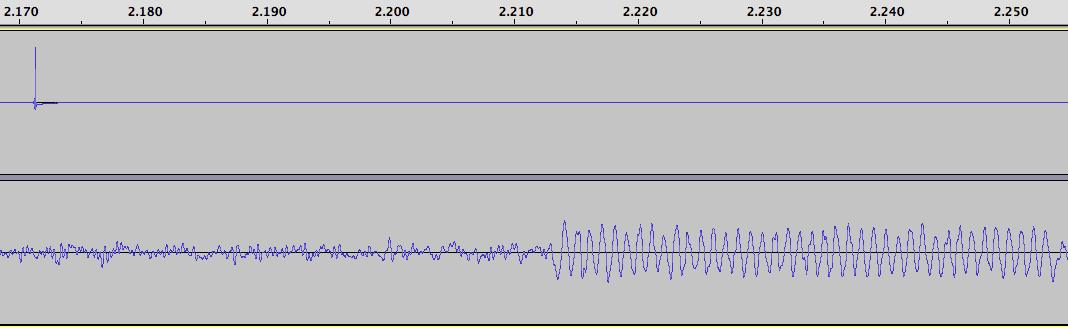
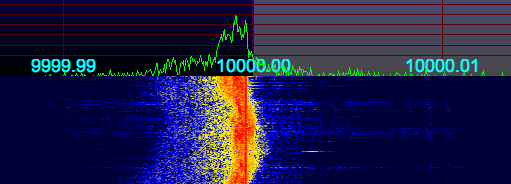
I fed the same 1 PPS signal into the antenna jack of the radio. The signal is a short (10 microsecond pulse) that is rich in harmonics, so it produces a noticeable “tick” sound every second. I then recorded the audio from the radio, along with the 1 PPS signal fed into the other channel, and obtained this data (click on the graph to enlarge it):

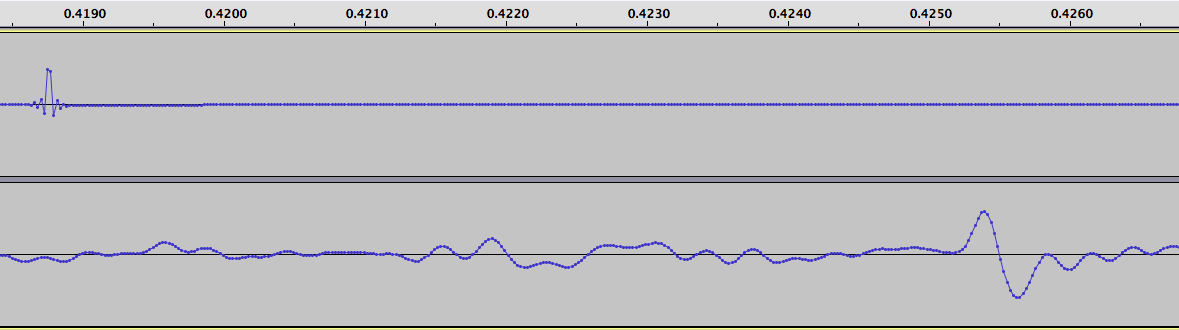
I measured the time delay between the two ticks, and found it to be 286 samples. At 44.1 kHz, each sound sample is 22.676 microseconds. Multiplication gives us the time delay, namely 6485 microseconds. This delay added by the radio is constant, provided I do not adjust the IF filtering parameters (which were set to USB mode, 4.0 kHz wide, for all tests).

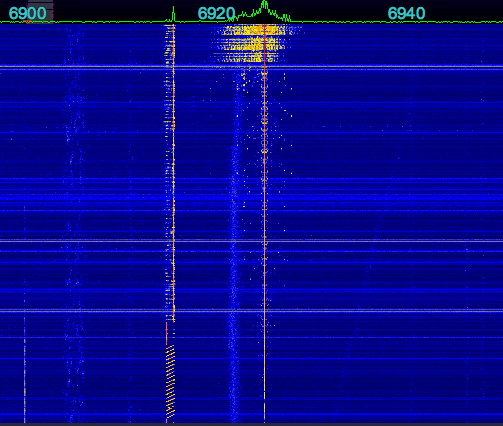
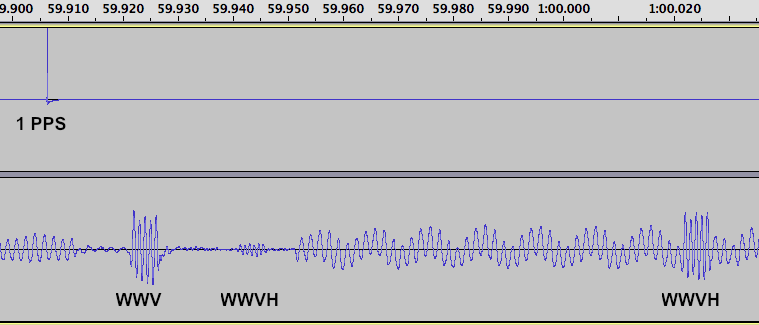
Next, the antenna was reconnected, an the radio tuned to 15 MHz. At this time of the day (about 2100 UTC) it is possible to hear both WWV and WWVH. Here’s the sound recording:

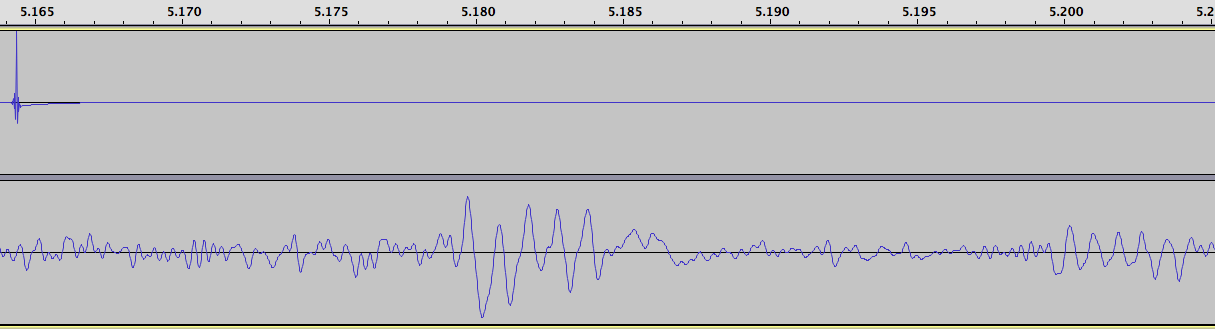
The WWV pulse occurs at about 5.18 seconds on the recording, and WWVH, much weaker and harder to see, at about 5.2 seconds.

The delay for the WWV pulse is 657 samples. Subtracting the radio delay of 286 gives us a delay due to propagation of 371 samples. Multiplying by our conversion factor of 22.676 microseconds per sample gives us 8413 microseconds.

Light (and radio waves) travel at 186,282 miles per second or about 0.186 miles per microsecond. For the metric inclined, that’s 299.792 km/sec or 0.300 km per microsecond. So multiplying our time in microseconds by the distance light travels each microsecond gives us the distance:

8413 * 0.186 = 1567 miles (2522 km)

The actual distance, along the Earth’s surface, from my location to WWV is 1480 miles, or 2382 km. Why the discrepancy? The radio waves do not travel along the Earth’s surface, but instead are reflected from the ionosphere, which is several hundred miles up. This means the actual path they take is longer. We’ll try to take that into account, a little further down.

The delay for the WWVH pulse is 1550 samples. Subtracting the radio delay of 286 gives us a delay due to propagation of 1264 samples. Multiplying by our conversion factor of 22.676 microseconds per sample gives us 28662 microseconds. We’ll do our next multiplication again, to convert to distance:

28662 * 0.186 = 5339 miles (8592 km)

The actual distance from my location to WWVH is 4743 miles, or 7633 km.

Next, here’s a recording from the Canadian time station, CHU:

The delay for the CHU pulse is 401 samples. Subtracting the radio delay of 286 gives us a delay due to propagation of 115 samples. Multiplying by our conversion factor of 22.676 microseconds per sample gives us 2607 microseconds. We’ll do our next multiplication again, to convert to distance:

2607 * 0.186 = 486 miles (782 km)

The actual distance from my location to CHU is 407 miles, or 656 km.

Now let’s try to take into account the actual path of the radio waves, which get reflected off the ionosphere. We need to know the height of the ionosphere, which unfortunately is not constant, nor is it the same over each part of the Earth. Here is a map showing the approximate height, while the above recordings were taken:

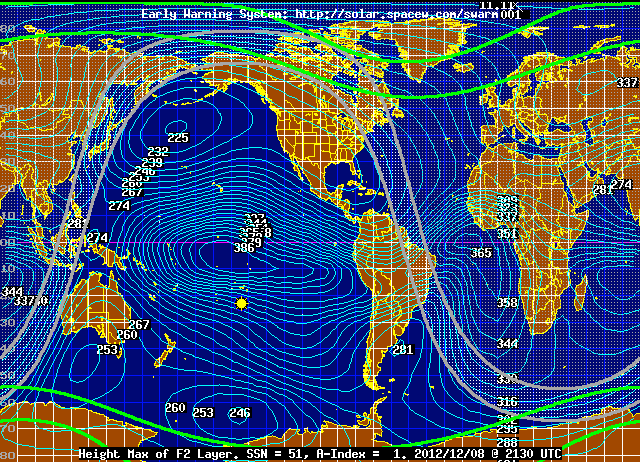
In the case of the path to CHU, the height is about 267 km, or 166 miles.

We also need to determine the straight line path between my location and CHU, through the Earth, vs the distance along the Earth’s surface. This can be calculated, and it is 391 miles, or 629 km.

We’ll determine what the actual path length is for a radio signal traveling this distance. It looks like a triangle, with a height of 166 miles, and a base of 391 miles. We need to determine the other two sides to find the total path length. All we need to do is take half of 391 miles, which is 195.5 miles, square it, add to that 166 squared, and take the square root, then double our answer. The result is 513 miles, which is very close to our measured value of 486 miles. We’re off by a little more than 5%.

Next let’s try WWV: The actual distance is 1468 miles or 2362 km. Doing our math, using an approximate FoF2 ionosphere height of 246 km (153 miles): Half of 1468 miles is 734 miles, we square that and add to 153 squared, and take the square root, and double our answer, getting 1500 miles. Our measured distance was 1567 miles, so we’re off by less than 5%.

Next, the case of WWVH. This is more complicated, as the signal probably is making more than one “hop”, that is, it is going up to the ionosphere, reflected down to Earth, and then reflected back up again, and down again. This may possibly occur multiple times.

We’ll try doing the math anyway. The actual distance is 4588 miles or 7383 km. Doing our math, using an approximate FoF2 ionosphere height of 253 km (157 miles): Half of 4588 miles is 2294 miles, we square that and add to 157 squared, and take the square root, and double our answer, getting 4598 miles. Our measured distance was 5339 miles, an error of 16%. But again, we don’t know how many hops there were. Still, not a bad effort.

Does anyone else have a GPS receiver with a 1 PPS output? If so, I’d like to hear from you, I have some additional experiments in mind.

Propagation Gives Away Your Location

Posted on by
1

Being as pirate radio is, well, illegal, operators like to stay anonymous. At least ops who want to avoid the FCC. Naturally, most ops consider keeping their location secret very important. Some even go so far as subtly, or not so subtly, providing false clues about their location, in an effort to fool the radio authorities. Unfortunately, basic rules of radio propagation make this futile.

A warning in advance. I’m going to be discussing some basic shortwave radio propagation theory. Nothing here is brand new, or unknown to anyone in the radio field. Certainly not the radio authorities. Some fur… err… feathers are possibly going to be ruffled by what is presented below, possibly with loud protests of “destroying pirate radio” and “releasing the identities of operators”. Nothing could be further from the truth. This is Propagation 101 stuff. If it scares you, then you probably shouldn’t be operating a pirate radio station. The purpose is the educate listeners and operators, so they know exactly what information can be gleaned from observing signal reports. It’s better to know exactly what can be done with this information, than to stick your head in the sand and pretend it doesn’t exist.

As has been discussed on this blog many times before, daytime propagation on the 43 meter band (where 6925 kHz is located) is considered NVIS (Near Vertical Incident Sky Wave). The radio waves go up, and are reflected back to the Earth for a fairly short distance around the transmitter site, usually a few hundred miles at the most. Attenuation by the D layer limits distant reception. At night, it’s almost the opposite reception pattern, as the D layer fades away, allowing distant reception. And the weaker F layer limits or eliminates NVIS reception, resulting in a skip zone around the transmitter, where the signal cannot be heard. The resulting reception area is shaped roughly like a doughnut.

So, for a daytime transmission, if one looks at a set of reception reports (as well as “no reception” reports, which can be equally useful), it becomes very easy to guesstimate about where a transmitter is. Not exactly of course, or even to a particular state, but certainly within a hundred miles or two. There will be a cluster of strong reception reports around the transmitter site, out to a few hundred miles. The maximum reception distance will vary a lot with transmitter level, antennas, and propagation conditions, but is likely under 1,000 miles. Look at where all the reports are coming from, especially the strong ones, find the center, and you have a good guess as to where the transmitter is.

At nighttime, listeners too close to the transmitter site (in the skip zone) will hear nothing, or at best a very weak signal. And during the transition from NVIS to DX propagation (see Going Long and An Interesting Example of a Station Going Long) the received signal will start to peak, and then suddenly cut out. Observing when this happens at a variety of listener sites provides other clues as to the transmitter location. If the F layer height and ionization values are known (and they are available in real time online) the distant to the station can be roughly determined when the station goes long. Do this for several receiver locations, and you can guess about where the transmitter is.

One ruse some operators have used in the past is to give misleading reception reports with a low signal level, using their real name and location, as just a regular listener. This is extremely dangerous, as if anyone is paying attention, their very weak signal report can stand out like a sore thumb if there are reports from others in the same area, with much stronger signal levels. Likewise, if you’re an operator, providing a completely bogus QTH doesn’t fool the FCC one bit. Announcing a QTH out on the Great Plains, while you’re really on the East Coast, doesn’t fool anyone when you’re being heard on the East Coast with an S9 signal at local noon. It just reminds everyone that you failed PROPAGATION 101. While shortwave propagation can be odd at times, there are limits. The laws of physics still must be obeyed.

The FCC and other radio enforcement agencies of course don’t have to rely on crude techniques such as these to locate transmitters. They have modern DFing equipment that can quickly and accurately locate a pirate station. The only reason they haven’t busted a given pirate is because, (as much as this may hurt to hear) that pirate is not important enough to get a visit. For now.

The commercially available WJ-9012 HF Direction Finding System, for example, boasts an error of less than 2 degrees. At a distance of 200 miles, that’s about 7 miles. Presumably the FCC has much better equipment.

While not announcing your location is probably a good idea (if for no other reason than to come across as taunting the FCC), in reality it doesn’t do too much to protect you from the radio authorities. Not interfering with allocated radio services, especially government and military, as well as operating from random remote locations, will go a long way to avoid getting The Knock.

Keep Safe!

Daytime Vs Nighttime Static Levels And The Impact On Reception

Posted on by
Reply

Undercover Radio was on 6925 kHz USB several times on Sunday, May 20, 2012, conducting some transmitter tests in the afternoon, and with a show in the evening. I noticed how, even with a relatively weak signal strength in the afternoon, the overall reception was still good, due to the low daytime noise levels on the 43 meter band. Transmitter power was around 20-30 watts PEP.

Here is a graph showing the signal level of Undercover Radio on 6925 kHz, as well as background noise from an otherwise unoccupied adjacent frequency for 4 minutes, starting at 1700 UTC May 20, 2012:

Undercover Radio’s signal strength was about -92 dBm. Bear in mind that this was a voice only program with Dr. Benway talking, with frequent pauses in speech. Since this was an SSB transmission, the received signal level falls to the background noise level during pauses in speech.

The background static at 6930 kHz was -100 dBm

The net result is a signal to noise ratio of 8 dB, which is certainly adequate for fair to good reception.

Some recordings:
Undercover Radio 6925 kHz USB 1700 UTC
Background noise 6930 kHz USB 1700 UTC

Undercover Radio came back on at around 1900 UTC. Here is another comparison of Undercover’s signal vs background noise on 6932 kHz:

(Sorry, this time the noise is pink and the signal is blue. Just to keep you on your toes)

Eyeballing the graphs, it looks like the signal to noise ratio was about 15 dB, better than before. The quality of the received audio was indeed very good. Here is a recording

Next, Undercover Radio came on again at 0212 UTC.

The noise levels were around -85 dBm. Undercover Radio’s signal started at just around the noise level. At the time, he was running 20-30 watts PEP. Later, around 0245, Dr Benway realized he didn’t have the amp on, and then switched it on, going to 500-600 watts PEP.

One reason for the much higher nighttime noise levels is that not only is 43 meters open to DX from distant stations, but also to distant thunderstorms and other noise sources. Think of every thunderstorm in the world as a transmitter (which it really is). There’s thousands of active thunderstorms at any time, transmitting RF energy over the entire radio spectrum. This energy is received at your location from whatever parts of the world propagation is open to, on a given frequency. So while your signal can get out further at nighttime, it also has to compete with a lot more QRM sources.

During the daytime, the D layer of the ionosphere attenuates low angle radiation on 43 meters, preventing DX reception. You’re limited to just a few hundred miles. This applies both to the signals from radio stations that we want to hear, and distant noise sources.

Also notice how much Undercover Radio’s signal varied after the amp was switched on – by around 30 dB. That’s five S units! This tells us that signal reports, or even recordings, can be very hit or miss. One minute, an op can be at the noise level, a few minutes later, he can be many S units above it.

Two recordings. First, one from 0222 UTC when he was running 20-30 watts PEP, and the SNR was just a few dB. And second, one from 0300 UTC during a signal peak, when he was running 500-600 watts PEP, and the SNR was about 25 dB.

For comparison, here are some plots of WWCR, 6875 kHz, showing their signal level last night:

First, from 2230 to 0100 UTC (sorry for the X axis scaling, showing -100 for 2300 UTC. Blame Excel)

You can see that when their carrier went off the air, the noise level was around -80 dBm. And the signal varies by about 30 dB during the transmission, during nighttime. Earlier in the transmission, while it was still daytime, the signal was slightly weaker, but there was a lot less fading.

And second at 0300 UTC:

Perhaps the main point to take away from this is that while a pirate can be heard much further at nighttime than during the daytime on 43 meters, the lower noise levels and lack of significant fading during the daytime generally make for better quality reception, for those listeners within the several hundred mile NVIS range, and allows reception by listeners with more modest receiver/antenna setups. This is especially true when using lower power (grenade type) transmitters. Nighttime DX reception quality will be poorer, and limited to those with more substantial receiving stations. By selecting the time of day for operation, operators can to some degree select their audience and target area. A pair of transmissions, one in the daytime and one at night, would reach both local and DX listeners.

Signal Levels of Radio True North’s May 14th Transmission on 6950 kHz

Posted on by
Reply

The graph below shows the received signal levels of Radio True North, a pirate radio station from Canada, which transmitted on 6950 kHz on Mary 14, 2012. The signal faded in at around 0200 UTC, and the transmitter was switched off at 0702 UTC – that can plainly be seen on the chart:

You can also see that after the transmitter switched off, the received signal levels were about -85 dBm, that is the background noise level. At peak, the signal was about -75 dBm, just a hair under S9. The signal to noise ratio is the difference between the signal and noise levels, or 10 dB.

Here is a short recording taken at around 0516 UTC, so you can hear what this signal sounds like. Remember, it is around S9, but the signal to noise ratio, which is what really matters, is only 10 dB. We had rain/thunder storms all along the east coast during this time.

Signal to noise ratios were discussed an earlier post, coincidently enough called Signal To Noise Ratios. There’s some simulated SNR recordings there. The 10 dB example sounds very close to the RTN recording above.

RTN was using his “usual power” (we’ll be vague and say a few hundred watts). Had he been using a lower power level, say 10 watts, the signal to noise ratio would have been about 0 dB, if not negative. He’s using a delta loop antenna, and is about 4,000 km (2,500 miles) away from my location.

Here’s a graph of RTN’s carrier frequency, as measured here:

You can observe both the power on drift, and short term cycling (about every 10 minutes) due to most likely to something thermal, perhaps a fan.

GPS Disciplined 10 MHz Reference

Posted on by
1

Some time ago, I wrote about the Rubidium reference that I connected to SDR. The reference supplies a very stable and precise 10 MHz reference clock to the SDR, so that the sample rate does not drift. Drift in the sample rate causes drift in the received frequency, much like drift in the various oscillators in a conventional radio causes drift.

Just today, I replaced the Rubidium reference with a GPS disciplined reference.

Here’s what I got:

The reference itself is the box in the center. To the right is the power supply, to the left is the antenna.

A GPS disciplined reference or oscillator uses timing signals from the GPS satellites to control,or “discipline” the oscillator built into the reference using a tracking loop. The 10 MHz output is continuously adjusted to keep it at the correct frequency, usually by making very small adjustments and using long time constants (averaging periods), typically around 100 seconds or more.

The 10 MHz output from the reference connects to an input on the netSDR. Internally, that 10 MHz signal is used to produce an 80 MHz clock that is used to drive the A/D sampling.

Here is what the inside of the reference looks like:

Here’s a plot of WWV on 10 MHz:

I believe the frequency shifts you see are due to doppler effects in the ionosphere.

Now I can figure out exactly what frequency Captain Morgan is on.